LHC Cavity Loop

Authors

Helga Timko

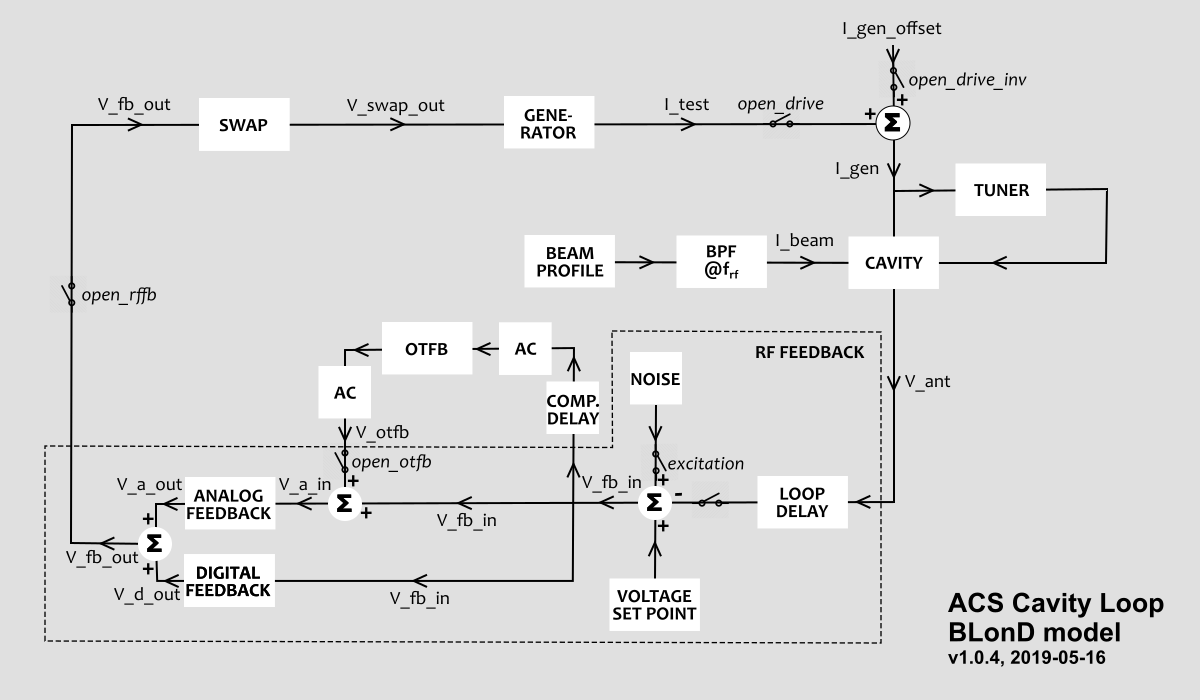
The interaction of the LHC cavity loop with the beam is modelled on a turn-by-turn basis. All arrays inside the class blond.llrf.cavity_feedback.LHCCavityLoop are complex arrays with a memory of exactly 2 turns (previous and present). The signals are digitised with a sampling time \(T_s\) that adapts to the revolution period to have exactly

N = int(self.rf.harmonic[0, 0]/10)

samples over one turn. The feedback is pre-tracked without beam.

STEP 1: Calculate RF beam current

The RF beam current is calculated for the entire turn, based on the beam profile \(\lambda_k\), where the sampling time is typically much smaller than T_s.

STEP 2: Cavity-generator-beam interaction

Within one turn, the update of parameters happens sample by sample, for \(n = 0...N-1\). First, the antenna voltage measured in the RF cavity \(V_{\mathsf{ant}}\) is updated based on the time evolution derived in [JT2011]

\[I_{\mathsf{gen}}(t) = \frac{V_{\mathsf{ant}}(t)}{2 R/Q} \left( \frac{1}{Q_L} - 2 i \frac{\Delta \omega}{\omega} \right) + \frac{d V_{\mathsf{ant}}(t)}{dt} \frac{1}{\omega R/Q} + \frac{1}{2} I_{\mathsf{beam,RF}}(t)\]

Here \(I_{\mathsf{gen}}\) is the generator forward current, \(I_{\mathsf{beam,RF}}\) is the RF beam current, \(R/Q\) is the cavity’s ratio of shunt impedance and quality factor, \(Q_L\) the loaded quality factor, \(\omega\) the rf frequency, and \(\Delta \omega \equiv \omega_c - \omega\) the detuning of the cavity w.r.t.the central frequency \(\omega_c\). In the discrete implementation, the equation reads as follows:

\[V_{\mathsf{ant}}^{(n)} = \frac{R}{Q} \omega T_s \, I_{\mathsf{gen}}^{(n-1)} + \left( 1 - \frac{\omega T_s}{2 Q_L} + i \Delta \omega T_s \right) V_{\mathsf{ant}}^{(n-1)} - \frac{1}{2} \frac{R}{Q} \omega T_s \, I_{\mathsf{beam,RF}}^{(n-1)} \, ,\]

where the upper indices denote the sample number.

STEP 3: RF feedback response

The RF feedback acts on the difference between measured antenna voltage and required set point voltage \(V_{\mathsf{set}}\):

\[V_{\mathsf{fb,in}}^{(n)} = V_{\mathsf{set}}^{(n)} - V_{\mathsf{ant}}^{(n - n_{\mathsf{loop}})} \, ,\]

where the overall loop delay \(\tau_{\mathsf{loop}}=650 \mathsf{ns}\) is taken into account in the antenna signal delayed by \(n_{\mathsf{loop}} \equiv int(\tau_{\mathsf{loop}})/T_s\).

Analog feedback

The analog feedback has a gain \(G_a\) at high frequencies and in Laplace domain its transfer function is:

\[\frac{Y(s)}{X(s)} = H_a(s) = G_a \frac{\tau_a s}{1 + \tau_a s} ,\]

where \(X(s)\) and \(Y(s)\) are the input and output signals, respectively. In the LHC, the typical delay is \(\tau_a = 170 \mathsf{\mu s}\) (based on AC coupling at demodulator exit), and the optimum gain for a flat closed- loop response is

\[G_a = \frac{1}{2\frac{R}{Q} \omega \tau_{\mathsf{loop}}} \, ,\]

which for a loop delay of \(\tau_{\mathsf{loop}} = 650 \mathsf{ns}\) results in \(G_a = 6.79 \times 10^{-6} \mathsf{\frac{A}{V}}\). Note that \(G_a\) converts the voltage signal to a current signal.

In discrete time domain, the output signal \(y(t)\) is calculated from the input signal \(x(t)\) as follows:

\[y^{(n)} = \left[ 1 - \frac{T_s}{\tau_a} \right] \, y^{(n-1)} + G_a(x^{(n)} - x^{(n-1)})\]

Digital feedback

The digital feedback, opposite to the analog feedback, has a high gain at low frequencies,

\[\frac{Y(s)}{X(s)} = H_d(s) = G_a G_d \frac{e^{i \Delta \varphi_{\mathsf{ad}}}}{1 + \tau_d s} ,\]

where the digital gain is typically \(G_d=10\), and the dephasing between the analog and digital feedbacks is to be minimized, \(\Delta \varphi_{\mathsf{ad}} \approx 0\).

In discrete time domain, the signal reads as

\[y^{(n)} = \left[ 1 - \frac{T_s}{\tau_d} \right] \, y^{(n-1)} + G_a G_d e^{i \Delta \varphi_{\mathsf{ad}}} \frac{T_s}{\tau_d} \, x^{(n-1)}\]

One-turn feedback

There is the possibility to switch on the one-turn feedback to boost the gain of the analog feedback. On the branch of the one-turn feedback (OTFB), there is a delay that is complementary to the total loop delay as seen by the OTFB \(\tau_{\mathsf{otfb}}\), \(T_0 - \tau_{\mathsf{otfb}}\), where \(T_0\) is the revolution period in that turn.

The response of the one-turn feedback itself reads as follows:

\[\frac{Y(s)}{X(s)} = H_{\mathsf{OTFB}}(s) = G_o \frac{(1 - \alpha) e^{-T_0s}}{1 - \alpha e^{-T_0s}} \, ,\]

where \(G_o = 10\) and \(\alpha=15/16\) usually.

In time domain, the signal from the previous turn is used to construct the signal at the current turn,

\[y^{(n)} = \alpha y^{(n - N)} + G_o (1 - \alpha) x^{(n - N)} \, .\]

Both at the input and the output, an AC coupling ensures that unwanted frequencies are filtered out,

\[\frac{Y(s)}{X(s)} = H_{\mathsf{AC,OTFB}}(s) = \frac{\tau_o s}{1 + \tau_o s}\]

where the time constant is around \(\tau_o=110 \mathsf{\mu s}\).

In time domain, this reads as

\[y^{(n)} = \left[ 1 - \frac{T_s}{\tau_o} \right] \, y^{(n - 1)} + x^{(n)} - x^{(n - 1)} \, .\]

In addition, a 63-tap finite-impulse response (FIR) filter is used to limit the bandwidth of the overall response.

The numerical implementation thus consists of the following four steps, in the below-mentioned order:

1. AC coupling at input on the signal of the previous turn, combined with OTFB delay \(T_0 - \tau_{\mathsf{otfb}}\) at input,

\[ y^{(n - N)} = \left[ 1 - \frac{T_s}{\tau_o} \right] \, y^{(n - N - 1)} + x^{(n - N + n_{\mathsf{otfb}})} - x^{(n - N + n_{\mathsf{otfb}} - 1)} \,\]

where \(N = \mathsf{int}(T_0/T_s)\) and \(n_{\mathsf{otfb}} = \mathsf{int}(\tau_{\mathsf{otfb}}/T_s + n_\mathsf{taps} - 1)/2)\), with \(n_\mathsf{taps}\) being the number of taps of the FIR filter,

2. OTFB response,

\[z^{(n)} = \alpha z^{(n - N)} + G_o (1 - \alpha) y^{(n - N)}\]

3. FIR filter response; N.B. this introduces an extra delay of \((n_\mathsf{taps} - 1)/2\) which is already compensated in step 1.

\[v^{(n)} = b_0 z^{(n)} + b_1 z^{(n-1)} + ... + b_{n_\mathsf{taps}} z^{(n - n_\mathsf{taps})}\]

4. AC coupling at output.

\[w^{(n)} = \left[ 1 - \frac{T_s}{\tau_o} \right] \, w^{(n - 1)} + v^{(n)} - v^{(n - 1)}\]

STEP 4: Switch and protect response

STEP 5: Generator response

STEP 6: Tuner control

References

JT2011

Joachim Tückmantel: ‘Cavity-beam-transmitter interaction formula collection with derivation’, CERN-ATS-Note-2011-002 TECH, CERN, Geneva, Switzerland, 2011.