Equations of Motion

Authors

Helga Timko

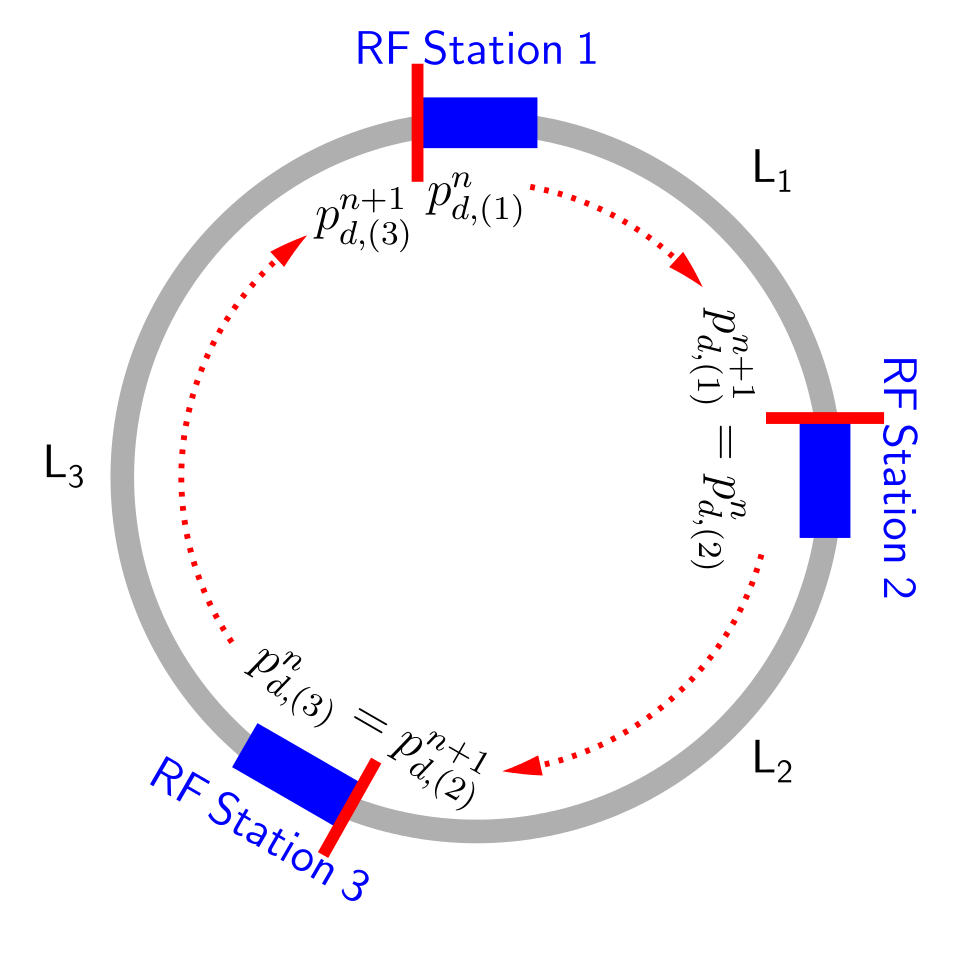
Below, we shall derive the equations of motion (EOMs) for an energy kick given to the particle by the RF caviti(es) of a given RF station and the subsequent drift of the particle during one turn, see Figure. In the case of multiple RF stations, the drift equation should be scaled by \(\frac{L_i}{C}\), where \(C = \sum_{i} L_i\) is the machine circumference.

Definitions

Code-internal units are SI-units unless otherwise specified in the below table.

Code-internal units

Energy \(E\) = [eV]

Momentum \(p\) = [eV]

Mass \(m\) = [eV]

Time \(t\) = [s]

Frequency \(f\) = [Hz]

Angular frequency \(\omega\) = [rad/s]

Just like in the real machine, we demand the user to define beforehand the energy programme, i.e. the synchronous (design) total energy at every time step \(n\) and RF station \((i)\), \(\left\{ E_{s,(i)}^n \right\}\). This will define the design momentum \(p_s\) through following relations:

(1)\[E_s = \gamma_s m ,\]

(2)\[p_s = \beta_s \gamma_s m ,\]

(3)\[E_s^2 = p_s^2 + m^2 ,\]

where \(m\) is the mass of the particle, and energy, momentum, and mass are given in [eV].

For a given synchronous orbit with an average radius \(R_s\), the angular frequency will be \(\omega_0 \equiv \frac{\beta_s c}{R_s}\) and one turn will take \(T_0 \equiv \frac{2 \pi}{\omega_0}\) at the synchronous energy. The magnetic field programme is assumed to be synchronised with the design energy turn by turn. Hence, a particle leaving the RF station with the synchronous energy will always be on the synchronous orbit and return to the RF station after exactly one period, unless the actual magnetic field differs from the designed one.

We define then an external reference (clock) time

(4)\[t_{\mathsf{ref}}^n \equiv \sum_{i=1}^n T_0^i ,\]

and as initial condition we choose the sinusoidal RF wave of the main RF system (harmonic \(h_0\) and RF frequency \(\omega_{\mathsf{rf},0}\)) to be at phase zero at time zero:

(5)\[V_{\mathsf{rf},0}(t) = V_0 \sin(\omega_{\mathsf{rf},0} \, t \, + \phi_{\mathsf{offset},0}) \Rightarrow \phi_{\mathsf{offset},0} (t=0) = 0.\]

All phase offsets of all RF systems are defined w.r.t. this initial condition and w.r.t. to the main RF system. Phase offsets can be programmed through the phi_offset parameter. In addition, RF phase noise \(\phi_{\mathsf{noise},k}\) can be added through phi_noise for each system. For \(n_{\mathsf{rf}}\) RF systems in the RF station the total voltage [eV] becomes:

(6)\[V_{\mathsf{tot}}(t) = \sum_{k=0}^{n_{\mathsf{rf}}-1} V_k \sin(\omega_{\mathsf{rf},k} \, t + \phi_{\mathsf{offset},k}^n + \phi_{\mathsf{noise},k}^n) .\]

We define the arrival time of an arbitrary particle to the RF station relative to the reference time in that turn,

(7)\[\Delta t^n \equiv t^n - t_{\mathsf{ref}}^n .\]

The total phase offset at the reference time is tracked in the variable phi_RF, defined through

(8)\[V_{\mathsf{tot}}(t=t_{\mathsf{ref}}^n) \equiv \sum_{k=0}^{n_{\mathsf{rf}}-1} V_k \sin(\phi_{\mathsf{rf},k}^n) .\]

Energy kick

During the passage through an RF station, the energy \(E^n\) of an arbitrary particle is changed by the total energy kick received from the various RF systems in the station. The energy change due to the induced electric fields in the magnets is negligible and beam-induced voltage is taken into account in the impedance module. The phase of the RF voltage of system k at the arrival time \(t^n\) of any particle is:

(9)\[\varphi_{\mathsf{rf},k}(t^n) = \int_{0}^{t^n} d\tau \, \omega_{\mathsf{rf}}(\tau) + \phi_{\mathsf{offset},k}^n + \phi_{\mathsf{noise},k}^n = \sum_{i=1}^{n} \omega_{\mathsf{rf},k}^i T_0^i + (t^n-t_{\mathsf{ref}}^n) \omega_{\mathsf{rf},k}^n + \phi_{\mathsf{offset},k}^n + \phi_{\mathsf{noise},k}^n .\]

Subtracting multiples of \(2 \pi\), which can be neglected,

(10)\[\varphi_{\mathsf{rf},k}(\Delta t^n) = \sum_{i=1}^{n} \frac{\omega_{\mathsf{rf},k}^i - h_k^i \omega_0^i}{h_k^i \omega_0^i} 2 \pi h_k^i + \omega_{\mathsf{rf},k}^n \Delta t^n + \phi_{\mathsf{offset},k}^n + \phi_{\mathsf{noise},k}^n .\]

Note that phi_RF is determined through the above equation,

(11)\[\phi_{\mathsf{rf},k}^n = \varphi_{\mathsf{rf},k}(\Delta t^n = 0) .\]

Thus the total energy change equation is

(12)\[E^{n+1} = E^{n} + \sum_{k=0}^{n_{\mathsf{rf}}-1} V_k^n \sin \varphi_{\mathsf{rf},k}(\Delta t^n)\]

Note

Eq. (12) is intrinsically discrete; no approximation has been done.

Note

The RF phase (Eq. (11)) differs from the sum of phase offset and phase noise only if the RF frequency differs from the design RF frequency \(\omega_{\mathsf{rf},k}^n \neq \Omega_{\mathsf{rf},k}^n \equiv h_k^n \omega_0^n\), i.e. when feedback loops are active.

Rather than the absolute energy, we are actually interested in the energy offset of a given particle w.r.t. the synchronous energy \(\Delta E^n \equiv E^n - E_s^n, \, \forall n\). So we choose our coordinate system to be centred around \(E_s^n \, \forall n\). Substracting \(E_s^{n+1}\) from both sides of Eq. (12), we arrive at

(13)\[\Delta E^{n+1} = \Delta E^{n} + \sum_{k=0}^{n_{\mathsf{rf}}-1} V_k^n \sin \varphi_{\mathsf{rf},k}(\Delta t^n) - (E_s^{n+1} - E_s^n) .\]

Warning

As a consequence, during acceleration the coordinate system is non-inertial and a coordinate transform is done turn by turn.

Arrival time drift

Frequency slippage

The frequency slippage of an off-momentum particle during one turn is defined w.r.t. the design synchronous particle,

(14)\[\frac{\Delta \omega}{\omega_0} = \frac{\omega - \omega_0}{\omega_0} \equiv - \eta(\delta) \delta = - (\eta_0 + \eta_1 \delta + \eta_2 \delta^2 + ...) \delta,\]

where \(\delta \equiv \frac{\Delta p}{p_s} = \frac{\Delta E}{\beta_s^2 E_s}\) is the relative off-momentum of the particle and \(\eta_i\) are the slippage factors

(15)\[\begin{split}\eta_0 = \alpha_0 - \frac{1}{\gamma_s^2} \\ \eta_1 = \frac{3 \beta_s^2}{2 \gamma_s^2} + \alpha_1 - \alpha_0 \eta_0 \\ \eta_2 = - \frac{\beta_s^2(5 \beta_s^2 - 1)}{2 \gamma_s^2} + \alpha_2 - 2 \alpha_0 \alpha_1 + \frac{\alpha_1}{\gamma_s^2} + \alpha_0^2 \eta_0 - \frac{3 \beta_s^2 \alpha_0}{2 \gamma_s^2},\end{split}\]

which are defined via the momentum compaction factors \(\alpha_i\).

The absolute arrival time of an arbitrary particle can be expressed as a recursion

(16)\[t^{n+1} = t^n + \frac{2 \pi}{\omega^{n+1}} ,\]

with initial condition \(t^0 = t_0\) and where the revolution frequency of the particle \(\omega^n \equiv \frac{\beta^n c}{R^n}\) can differ from \(\omega_0^n\) due to energy and orbit deviations from the synchronous particle.

Note

Eq. (16) contains \(\omega^{n+1}\) as we chose to perform the energy kick first and the subsequent time drift happens according to the already updated energy.

Using Eq. (7), the recursion on the particle arrival time relative to the clock becomes

(17)\[\Delta t^{n+1} = \Delta t^n + \frac{2 \pi}{\omega^{n+1}} - \frac{2 \pi}{\omega_0^{n+1}} = \Delta t^n + T_0^{n+1} \left( \frac{1}{\frac{\omega^{n+1}}{\omega_0^{n+1}}} - 1 \right)\]

Using definition (14), the arrival time drift can be calculated as

(18)\[\Delta t^{n+1} = \Delta t^n + T_0^{n+1} \left( \frac{1}{1 - \eta(\delta^{n+1})\delta^{n+1}} - 1 \right) .\]

If a zeroth order slippage is used, \(\eta(\delta) \approx \eta_0\), the option solver = 'simple' can be used to approximate the above equation as

(19)\[\Delta t^{n+1} = \Delta t^n + \frac{\eta_0^{n+1} T_0^{n+1}}{(\beta_s^{n+1})^{2} E_s^{n+1}} \Delta E^{n+1} .\]

In a newer implementation of the drift equation, default since 2020, we use the momentum compaction factors directly, instead of the slippage factors, to calculate the time slippage,

(20)\[\Delta t^{n+1} = \Delta t^n + T_0^{n+1} \left[(1 + \alpha_0^{n+1}\delta^{n+1} + \alpha_1^{n+1}(\delta^{n+1})^2 + \alpha_2^{n+1}(\delta^{n+1})^3) \left( \frac{1 + \frac{\Delta E^{n+1}}{E_s^{n+1}}}{1 + \delta^{n+1}} \right) - 1 \right]\]

The synchronous particle

A particle is synchronous in turn n if it enters and leaves the RF station with zero energy offset, \(\Delta E^n = \Delta E^{n+1} = 0\), and thus gains exactly the designed energy gain \(E_s^{n+1} - E_s^n\). As a consequence, in the absence of induced voltage the synchronous particle will fulfil:

(21)\[\sum_{k=0}^{n_{\mathsf{rf}}-1} V_k^n \sin \varphi_{\mathsf{rf},k}(\Delta t_s^n) = (E_s^{n+1} - E_s^n) ,\]

and in the presence of intensity effects, the induced voltage from the particles in front should be added on the left-hand side:

(22)\[\sum_{k=0}^{n_{\mathsf{rf}}-1} V_k^n \sin \varphi_{\mathsf{rf},k}(\Delta t_s^n) - e \int_{\Delta t_{\mathsf{min}}}^{\Delta t_s^n} d\tau \lambda(\tau) W(\Delta t_s^n - \tau) = (E_s^{n+1} - E_s^n) ,\]

where \(\lambda(t)\) is the beam/bunch profile and \(W(t)\) the wake potential.

See also

http://dquartul.github.io/BLonD/impedances.html

Warning

In general, these equations have \(n_{\mathsf{rf}}\) solutions. If the synchronous energy gain \(E_s^{n+1} - E_s^n\) changes from one turn to another, also the synchronous particle changes with it.

Note

Synchronous particle arrival time

As a consequence, the arrival time of the synchronous particle \(\Delta t_s\) is not necessarily constant, but can change from turn to turn. This might be counter-intuitive, as the synchronous particle drifts with exactly \(\omega_0\) along the ring. To see this effect, consider two subsequent turns with different synchronous energy gains \(E_s^{n+1} - E_s^{n} \ne E_s^{n+2} - E_s^{n+1}\) in a single-RF system. Let particle 1 be synchronous in turn n and particle 2 be synchronous in turn \(n+1\):

(23)\[\begin{split}\Delta E_1^n = \Delta E_1^{n+1} = 0 \,\,\, \ne \Delta E_1^{n+2} \\ \Delta t_1^{n-1} = \Delta t_1^n = \Delta t_1^{n+1} \,\,\, \ne \Delta t_1^{n+2}\end{split}\]

(24)\[\begin{split}\Delta E_2^n \ne \,\,\, \Delta E_2^{n+1} = \Delta E_2^{n+2} = 0 \\ \Delta t_2^{n-1} \ne \,\,\, \Delta t_2^n = \Delta t_2^{n+1} = \Delta t_2^{n+2}\end{split}\]

The arrival time of the synchronous particles in this case will be:

(25)\[\begin{split}\Delta t_s^n \equiv \Delta t_1^n \\ \Delta t_s^{n+1} \equiv \Delta t_2^{n+1}\end{split}\]

Thus, because the synchronous particle can be a different particle each turn, the recursion on the synchronous arrival time becomes in general

(26)\[\Delta t_s^{n+1} = \Delta t_s^n + (\Delta t_2^{n+1} - \Delta t_1^n) = \Delta t_s^n + (\Delta t_2^n - \Delta t_1^n) .\]

The difference in arrival time of the two particles in turn n can be determined from the energy equations

(27)\[\begin{split}V^n \sin \left( \omega_{\mathsf{rf}}^n \Delta t_1^n + \varphi_{\mathsf{rf}}^n \right)= (E_s^{n+1} - E_s^n) \\ V^{n+1} \sin \left( \omega_{\mathsf{rf}}^{n+1} \Delta t_2^{n+1} + \varphi_{\mathsf{rf}}^{n+1} \right) = V^{n+1} \sin \left( \omega_{\mathsf{rf}}^{n+1} \Delta t_2^n + \varphi_{\mathsf{rf}}^{n+1} \right) = (E_s^{n+2} - E_s^{n+1}) ,\end{split}\]

which in first-order approximation (see Small-amplitude oscillations) gives

(28)\[\sin{\varphi_s^{n+1}} - \sin{\varphi_s^n} \approx ( \omega_{\mathsf{rf}}^{n+1} \Delta t_2^n + \varphi_{\mathsf{rf}}^{n+1} - \omega_{\mathsf{rf}}^n \Delta t_1^n - \varphi_{\mathsf{rf}}^n) \cos{\varphi_s^n} = \frac{E_s^{n+2} - E_s^{n+1}}{V^{n+1}} - \frac{E_s^{n+1} - E_s^{n}}{V^{n}} .\]

Small-amplitude oscillations

Assuming a single-RF station and a simple solver (Eq. (19)), the EOMs in continous time can be written as

(29)\[\Delta \dot{E} = \frac{V}{T_0} \left( \sin(\omega_{\mathsf{rf}} \Delta t + \varphi_{\mathsf{rf}}) - \sin{\varphi_s} \right),\]

(30)\[\Delta \dot{t} = \frac{\eta_0}{\beta_s^2 E_s} \Delta E .\]

Assuming further a constant synchronous phase \(\sin{\varphi_s} \equiv \frac{\dot{E_s}}{V}\) and expanding the RF wave around it

(31)\[\omega_{\mathsf{rf}} \Delta t + \varphi_{\mathsf{rf}} = \varphi_s + (\omega_{\mathsf{rf}} \Delta t + \varphi_{\mathsf{rf}} - \varphi_s) \equiv \varphi_s + \varepsilon , \,\,\, \varepsilon \ll 1 ,\]

we obtain for the sinusoidal term in first order

(32)\[\sin (\omega_{\mathsf{rf}} \Delta t + \varphi_{\mathsf{rf}}) = \sin {\varphi_s} \cos{\varepsilon} + \cos{\varphi_s} \sin{\varepsilon} \approx \sin{\varphi_s} (1 + \mathcal{O}(\varepsilon^2)) + \cos{\varphi_s} (\varepsilon + \mathcal{O}(\varepsilon^3)) .\]

Derivating Eq. (29) a second time, and using Eq. (30)

(33)\[\Delta \ddot{E} = \frac{V \cos{\varphi_s} \, \omega_{\mathsf{rf}}}{T_0} \Delta \dot{t} = \frac{V \eta_0 \cos{\varphi_s} \, \omega_{\mathsf{rf}} \omega_0 }{2 \pi \beta_s^2 E_s} \Delta E .\]

Vice versa, derivating (30) another time, and substituting Eq. (29), an equivalent equation can be found for the arrival time w.r.t. to the arrival of the synchronous particle \(\Delta t_s\):

(34)\[\Delta \ddot{t} - \Delta \ddot{t_s} = \frac{V \eta_0 \cos{\varphi_s} \, \omega_{\mathsf{rf}} \omega_0 }{2 \pi \beta_s^2 E_s} (\Delta t - \Delta t_s) .\]

Equations (33) and (34) describe an oscillating motion in phase space if \(\eta_0 \cos{\varphi_s} < 0\), which for \(\omega_{\mathsf{rf}} = h \omega_0\) has the synchrotron frequency

(35)\[\omega_{s,0} = \sqrt{\frac{- h V \eta_0 \cos{\varphi_s}}{2 \pi \beta_s^2 E_s}} \omega_0 .\]

Note

that energy and time are conjugate variables, whereas energy and phase are not. When forming time derivatives in phase, one should take into account the frequency correction from one turn to another: \(\dot{\varphi} \approx \varphi^{n+1} - \frac{\omega_{\mathsf{rf}}^{n+1}}{\omega_{\mathsf{rf}}^n} \varphi^n\).

Tracking utilities

Hamiltonian

To construct the Hamiltonian \(\mathcal{H}\) from the conjugate variables \(\Delta t\) and \(\Delta E\), let us first rewrite the equations of motion in continuous time (for a zeroth-order slippage factor):

(36)\[\dot{\Delta t} = \frac{\Delta t^{n+1} - \Delta t^n}{T_0^{n+1}} = \frac{\eta_0}{\beta_s^2 E_s} \Delta E = \frac{\partial \mathcal{H}}{\partial (\Delta E)} ,\]

(37)\[\dot{\Delta E} = \frac{\Delta E^{n+1} - \Delta E^n}{T_0^{n+1}} = \sum_{k=0}^{n_{\mathsf{rf}}-1} \frac{q V_k}{T_0} \sin (\omega_{\mathsf{rf}}^k \Delta t + \varphi_{\mathsf{rf}}^k) - \dot{E_s} = - \frac{\partial \mathcal{H}}{\partial (\Delta t)} ,\]

from which we obtain the Hamiltonian by partial integration:

\[\mathcal{H}(\Delta t, \Delta E) = \int d(\Delta t) \partial_{\Delta t} \mathcal{H} + \int d(\Delta E) \partial_{\Delta E} \mathcal{H} = \int d(\Delta E) \dot{\Delta t} - \int d(\Delta t) \dot{\Delta E} ,\]

\[\mathcal{H}(\Delta t, \Delta E) = \frac{\eta_0}{2 \beta_s^2 E_s}(\Delta E)^2 + \sum_{k=0}^{n_{\mathsf{rf}}-1} \frac{q V_k}{T_0 \omega_{\mathsf{rf}}^k} \cos (\omega_{\mathsf{rf}}^k \Delta t + \varphi_{\mathsf{rf}}^k) + \dot{E_s} \Delta t + \mathsf{const} .\]

The constant of integration can be chosen such that

\[\mathcal{H}(\Delta t = \Delta t_s, \Delta E = 0) = 0 ,\]

from which the Hamiltonian becomes

\[\mathcal{H}(\Delta t, \Delta E) = \frac{\eta_0}{2 \beta_s^2 E_s}(\Delta E)^2 + \sum_{k=0}^{n_{\mathsf{rf}}-1} \frac{q V_k}{T_0 \omega_{\mathsf{rf}}^k} \left( \cos (\omega_{\mathsf{rf}}^k \Delta t + \varphi_{\mathsf{rf}}^k) - \cos (\omega_{\mathsf{rf}}^k \Delta t_s + \varphi_{\mathsf{rf}}^k) \right) + \dot{E_s} (\Delta t - \Delta t_s) .\]

In case of a single-harmonic RF system with \(\omega_{\mathsf{rf}} = h \omega_0\), the second term can be replaced with \(\dot{E_s} = q V \sin{\varphi_s} / T_0\), and we obtain the know textbook formula

\[\mathcal{H}(\Delta t, \Delta E) = \frac{\eta_0}{2 \beta_s^2 E_s}(\Delta E)^2 + \frac{q V}{2 \pi h} \left( \cos (h \omega_0 \Delta t + \varphi_{\mathsf{rf}}) - \cos (h \omega_0 \Delta t_s + \varphi_{\mathsf{rf}}) + h \omega_0 (\Delta t - \Delta t_s) \sin{\varphi_s} \right) ,\]

or in terms of particle phase \(\varphi\),

\[\mathcal{H}(\varphi, \Delta E) = \frac{\eta_0}{2 \beta_s^2 E_s}(\Delta E)^2 + \frac{q V}{2 \pi h} \left( \cos \varphi - \cos \varphi_s + (\varphi - \varphi_s) \sin{\varphi_s} \right) .\]

Separatrix

To construct the separatrix, first the unstable fixed point (UFP) needs to be determined. Its coordinates \((\Delta t_{\mathsf{ufp}}, \Delta E = 0)\) are calculated numerically by looking for the smallest (largest) zero crossing position in one period of the total voltage waveform above (below) transition. The separatrix is the equipotential line that goes through the UFP and is thus defined by the condition

\[\mathcal{H}(\Delta t_{\mathsf{ufp}}, \Delta E = 0) = \mathcal{H}(\Delta t_{\mathsf{sep}}, \Delta E_{\mathsf{sep}}) .\]

Solving this equation we obtain

\[\Delta E_{\mathsf{sep}} = \pm \sqrt{ \frac{2 \beta_s^2 E_s}{\eta_0} \left \{ \sum_{k=0}^{n_{\mathsf{rf}}-1} \frac{q V_k}{T_0 \omega_{\mathsf{rf}}^k} \left [ \cos (\omega_{\mathsf{rf}}^k \Delta t_{\mathsf{ufp}} + \varphi_{\mathsf{rf}}^k) - \cos (\omega_{\mathsf{rf}}^k \Delta t_{\mathsf{sep}} + \varphi_{\mathsf{rf}}^k) \right ] + \dot{E_s} (\Delta t_{\mathsf{ufp}} - \Delta t_{\mathsf{sep}}) \right \}} .\]

In the case of a single-harmonic RF system with \(\omega_{\mathsf{rf}} = h \omega_0\), the phase of the UFP is \(\varphi_{\mathsf{ufp}} = \pi - \varphi_s\). In addition, \(\dot{E_s} = q V \sin{\varphi_s} / T_0\), so the above equation reduces to

\[\Delta E_{\mathsf{sep}} = \pm \sqrt{ \frac{2 \beta_s^2 E_s q V}{2 \pi h \eta_0} \left \{ \cos (\pi - \varphi_s) - \cos \varphi + (\pi - \varphi_s - \varphi) \sin \varphi_s \right \} }.\]

In practise, to calculate the separatrix for input arrays \(\Delta t_{\mathsf{sep}}\) that are longer than the period of the voltage waveform, the routine takes into account periodicity and projects the input array onto the ‘basic period’ of the waveform (that is \((-\pi,\pi)\) and \((0,2 \pi)\) on the first harmonic, below and above transition, respectively).